Vào thời điểm kết thúc năm 1999 cận kề, truyền thông thế giới dần dần quan tâm hơn đến khái niệm Y2K hay Lỗi Thiên Niên Kỷ. Mối quan tâm này tập trung vào con số không (0). Ban đầu, khi các lập trình viên viết mã máy điện toán điều khiển phần lớn những chức năng quan trọng hàng ngày như hệ thống giao thông và ngân hàng, họ tiết kiệm trong việc sử dụng không gian lưu trữ. Khi đề ngày tháng cho bất cứ quá trình chạy máy tính nào thì các lập trình viên chỉ đơn giản lưu trữ tất cả ngày tháng dưới dạng hai con số thay vì bốn, ví dụ như 65 thay vì 1965. Họ chưa bao giờ lường trước các vấn đề có thể xảy ra khi 1999 chuyển sang năm 2000.
Số Không – hay 00 trong mã điện toán đối với máy tính – có nghĩa hoàn toàn khác với máy tính khi so với các lập trình viên. Đối với máy tính, 00 có thể có nghĩ là 1900 hoặc 1800 hay 2000. Cuối cùng thì, các lập trình viên có thể làm giảm thiểu vấn đề thảm họa tiềm tàng này và những ảnh hưởng của Lỗi Thiên Niên Kỷ thật sự không nghiêm trọng lắm. Tuy nhiên, giai thoại này là minh chứng cho cuộc vật lộn của con người đã có vài thiên niên kỉ nay với con số 0. Theo Brian Rotman: “số không liên quan mật thiết đến các khái niệm về sự hư vô, sự trống rỗng, khoảng trống. Để đọc, viết, nói về Hư Vô, hoặc để tin, hay tuyên bố như Socrates đã từng tuyên bố rằng [ông] không biết gì và để đến gần với khả năng hiển nhiên rằng mỗi chúng ta đều nằm trong sự huyễn hoặc tột bậc của, không phải Hư Vô, mà chẳng gì cả.”
Loài người vốn vẫn vật lộn với ý tưởng về “hư vô” từ khi chúng ta viết sử. Chúng ta có các ghi chép từ một số nền văn minh lớn cổ đại, cho thấy cách họ vật lộn với khái niệm số không qua khoa học toán học. Ngay cả khi dưới dạng một chữ số, số không vẫn bí ẩn và khó hiểu; tuy nhiên, chúng ta có thể lần theo nguồn gốc toán học và kiểm định tầm ảnh hưởng của nó lên những nền văn minh vĩ đại nhất, bao gồm cả thế giới hiện đại ngày nay.
Nguồn gốc ngôn từ
Từ “số không” có lẽ có nguồn gốc từ Ả Rập şifr, được La Tinh hóa thành zephirum bởi nhà toán học vĩ đại người Ý Fibonacci (nhũ danh là Leonardo of Pisa, 1175-1250). Các sách số học ở Ý sử dụng zephirum cho đến thời kỳ Phục Hưng. Trải qua một số thay đổi, nó đã trở thành zephiro và cuối cùng là zero, xuất hiện lần đầu tiên trong De Arithmetica opusculum (tạm dịch: Công trình số học) của Filippo Calandri được in tại Florence vào năm 1942 (Ifrah). Từ şifr là một từ Ả Rập, được dịch từ chữ Phạn sūnyā hay shunya có nghĩa là “trống rỗng.” Một cách dịch tương tự thời Trung cổ của şifr là cifra đã dẫn tới từ cipher (con số không) trong tiếng Anh hiện đại (Katz). Người Pháp vẫn còn dùng từ chiffre cho “number” hay “digit” còn người Đức là ziffer.
Số Không khi đó mô tả trạng thái trống rỗng và thể hiện vai trò là đại diện cho các con số. Nó không đại điện cho sự trống rỗng mà làm đầy sự trống rỗng đó (Boucenna).
Nguồn gốc Ai Cập, Sumer và Babylon
Con số không tiến hóa một cách độc lập ở ít nhất ở ba nền văn minh khác nhau và tách biệt về mặt địa lý: Babylon, Maya và Đông Ấn. Ở cả hai nền văn minh Babylon và Maya, con số không được xem là vật giữ chỗ (placeholder), một cách phân biệt giữa 1 và 100 trong hệ thống đếm dựa trên thang 10. Người Ai Cập cổ đại, người Sumer và Babylon ở phía Nam Mesopotamia (Iraq ngày nay), phát triển hệ thống đếm cổ nhất có niên đại gần 3000 năm trước công nguyên.
Người Ai Cập cổ đại sử dụng hệ đếm cơ số 10 (hệ thập phân) và có một loạt các biểu tượng phù hợp để biểu thị bằng hình ảnh các số như một, mười, một trăm, một ngàn, mười ngàn, một trăm ngàn và một triệu. Các biểu tượng từ một cho đến chín của người Ai Cập rất đơn giản và bao gồm một số lượng thích hợp các nét thẳng đứng được lặp đi lặp lại : ví dụ một là │và ba là │││. Các học giả Ai Cập biểu thị các con số lớn hơn chín sáng tạo hơn hẳn. Chữ U đảo ngược chỉ số mười, một trăm thì bằng cuộn xoáy, một ngàn là hoa sen, mười ngàn là một ngón cong, một trăm ngàn là một con ếch hay con nòng nọc có đuôi và một triệu là một người đàn ông với hai bàn tay hướng lên trời.
Vì người Ai Cập thể hiện những con số qua hình ảnh bằng chữ viết tượng hình, và những chữ viết này không mang bất cứ ý chỉ con số nào, cho nên mới thực sự không có nhu cầu về con số không. Người Ai Cập có ý tưởng về con số không, nhưng nó thiên về một vật giữ chỗ (placeholder) hơn là một con số, do đó, họ không có biểu tượng cho con số không.
Hệ thống đếm của người Babylon được sử dụng vào khoảng năm 3000 trước công nguyên. Nó phức tạp hơn hệ thống của người Ai Cập và được phát triển để đáp ứng nhu cầu có một hệ thống cho việc cai trị và tính toán, bởi vì người Babylon lưu giữ những bản ghi và sổ sách kế toán chi tiết về các trao đổi hàng hóa, các cửa hàng và tiền lương. Hệ thống này tận dụng vô cùng hiệu quả hệ thập phân, tương tự như của người Ai Cập, tuy nhiên, nó cũng đưa vào hệ cơ số 20 (hay hệ nhị thập phân), ví dụ như 60 là một cơ số được thêm vào. Chúng ta kế thừa hệ thống đếm thời gian ngày nay từ người Babylon: 60 giây một phút và 60 phút một giờ. Người Babylon sử dụng cả hai hệ cơ số để dễ dàng hơn khi viết đến 60 và hơn thế.
Vào khoảng 2600 năm trước công nguyên, người Babylon sáng tạo ra bút trâm hình nêm, cho ra những nét bút sắc hơn và cho phép viết những ký tự hình nêm. Hình thức này được biết đến là chữ hình nêm (cuneiform). Bằng cách sử dụng chữ hình nêm, các học giả Baybylon chỉ sử dụng hai dấu số: một hình nêm thẳng đứng (<) để thể hiện số một, và mộthình chữ V ngược (Λ) đại diện cho 10. Các học giả sử dụng hai ký hiệu 1 để biểu thị cho 2, ba ký hiệu 1 là ba và cứ tiếp tục như vậy đến 10. Sau 10, những người ghi chép của Babylon xoay bút trâm, vẽ biểu tượng hình chữ V ngược và bắt đầu viết các biểu tượng này để tạo ra các con số. Do đó, mười một là mười và một, mười hai là mười và hai số một, và cứ tiếp tục như vậy.
Trong khi hệ chữ viết hình nêm cho phép biểu thị các con số bằng một hệ thống phức tạp hơn nhiều, những nhầm lẫn bắt đầu xuất hiện do sự mơ hồ của hệ chữ viết này. Ví dụ, con số 60 nhìn giống con số 1. Do đó, 101 có thể được viết là 1>1 hay 1 1. Mười một cũng có thể được viết giống như vậy. Các nhà ghi chép sách đôi khi để lại một khoảng trống hay khoảng tách biệt giữa hai con số, ví dụ, 1 1 là 101, nhưng đôi khi họ không cẩn thận và quên phải để lại khoảng trống. Các nhà ghi chép của người Babylon có thể thực hiện nhiều phép tính phức tạp, và họ thực hiện rất tốt trong việc phát triển một hệ đếm dùng vị trí với các con số được sắp xếp vào các cột; tuy nhiên, họ không bao giờ phát triển hoàn toàn con số không, ngoài một vật giữ chỗ.
Nguồn gốc Maya
Ở phía bên kia địa cầu, vào khoảng năm 400 năm trước công nguyên, nền văn minh Maya phát triển rực rỡ tại Mexico ngày nay. Họ phát triển một hệ thống đếm dựa trên 20 (hệ nhị thập phân) và biểu thị số không bằng chữ tượng hình – một vỏ sò hình con mắt được sơn đỏ (Joseph). Người Maya biểu thị con số không dưới dạng hình ảnh là hình bầu dục với các đường cong nhỏ.
Người Maya viết các chữ số bằng cách sẽ dụng một chuỗi các chấm nhỏ (mỗi chấm biểu thị cho số một) và các que (mỗi que thể hiện cho số năm). Do đó, các chữ số viết của người Maya trông giống như các tháp xếp chồng lên nhau với tầng dưới cùng biểu thị các bội số của một và tầng trên là các bội số của 20. Bằng cách này, họ thêm hình vỏ sò để biểu thị con số không.
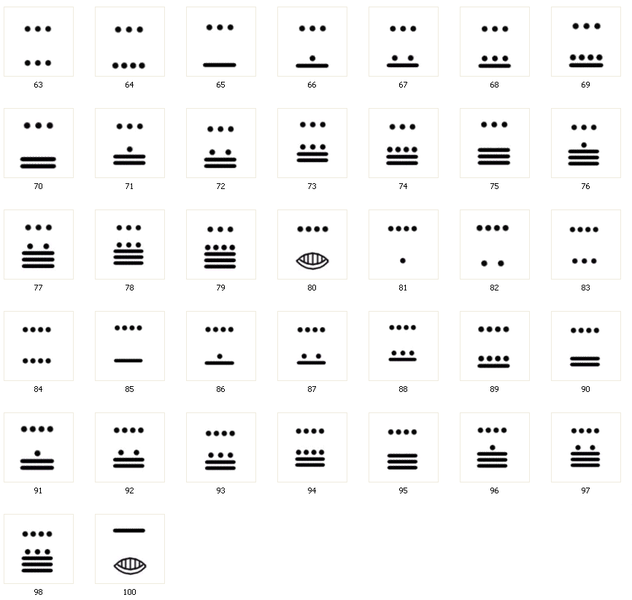
Tuy vậy, với vai trò là một con số, số không chưa bao giờ quan trọng đối với người Maya. Họ không hề có nhu cầu sử dụng con số không để ghi chép ngày tháng, hay cho bất kì phép toán hoặc chức năng khoa học nào khác; do vậy, con số không chưa bao giờ có vai trò gì hơn là một vật giữ chỗ. Cũng như người Ai Cập và người Babylon, người Maya dường như phát triển con số không vì lý do thẩm mỹ.
Cũng như người Ai Cập và người Babylon, người Maya dường như phát triển con số không vì lý do thẩm mỹ.
Nguồn gốc Ấn Độ: Cột mốc quan trọng đối với hệ thống số hiện đại của chúng ta
Trong From One to Zero (tạm dịch: Từ Một đến Không), Georges Ifrah viết: “Con số không ngày nay của chúng ta, hậu duệ trực tiếp của con số không Ấn Độ, rõ ràng là hơn hẳn hai số không còn lại (của Maya và Babylon).” Ông đưa ra phát biểu này bởi vì số không với vai trò là một con số mà chúng ta biết ngày nay sẽ chẳng đạt được tiềm năng của mình, nếu không có hàng thế kỉ mò mẫm rút kinh nghiệm, suy nghĩ và phát minh của các nhà toán học Ấn Độ. Sự sụp đổ của hai nền văn minh Maya và Babylon đã ngăn cản các học giả của họ khỏi việc phát triển con số không đạt đến tiềm năng như con số không ta biết ngày nay. Từ thế kỉ 6 trước công nguyên, các học giả người Ấn Độ đã chuyển từ hệ Brahmi sang hệ thập phân. Hệ thập phân khai phá sự tồn tại của những con số riêng biệt từ chữ số 1 đến 9, ký hiệu ngắn gọn cho những chữ số lớn hơn và những từ chỉ số lớn hơn 10 (Barrow).
Một khi hệ thống này được đưa vào sử dụng, chỉ là vấn đề thời gian trước khi biểu tượng con số không xuất hiện. Ví dụ sớm nhất cho con số không của người Ấn Độ là vào khoảng năm 458 sau công nguyên trong một nghiên cứu về vũ trụ của đạo Jain1. Ban đầu, người Ấn Độ biểu thị số không là một dấu chấm, nhưng sau đó thay thế bằng biểu tượng 0. Nhà khoa học máy tính người Mỹ gốc Ấn Subhash Kak đã đề xuất rằng vòng tròn biểu tượng quen thuộc cho chữ số không (0) được phát triển từ biểu tượng Brahmi cho con số 10 (∞). Người Ấn sử dụng con số không để đánh dấu thiếu vào sổ kế toán cho bất kì vị trí nào (hàng trăm, hàng chục, hàng đơn vị) của một số thập phân và bởi vì hệ thập phân của người Ấn có mỗi mức lại gấp mười lần mức trước, con số không cũng đóng vai trò là toán tử2 (operator). Lần đầu tiên, việc đặt con số không ở cuối một chuỗi các con số đã ảnh hưởng đến phép nhân cho 10, điều này cũng tương tự đối với số học và toán học hiện đại.
Do đó, con số không nhanh chóng đạt được vị trí như một con số. Vào năm 628 sau công nguyên, nhà thiên văn học người Ấn Brahmagupra đã định nghĩa con số không là kết quả của việc trừ bất cứ số nào cho chính nó và bởi vì vậy, ông mô tả các quy tắc cộng, trừ, nhân và chia như sau:
Khi sūnyā được thêm vào hay bớt đi khỏi một con số thì con số đó vẫn giữ nguyên không đổi; và một con số được nhân với sūnyā thì sẽ trở thành sūnyā.
Chữ số không của người Ấn cũng thú vị vì chiều sâu khái niệm mà nó thể hiện. Nếu như con số không của người Babylon và người Maya là những vật giữ chỗ một chiều để ghi lại những chỗ trống trong sổ sách kế toán, thì các học giả Ấn Độ cố gắng định lượng khái niệm mà con số này thực sự phản ảnh: sự hư vô và sự trống rỗng. Sūnyā là một từ tiếng Phạn nhằm diễn tả chiều sâu triết học của hư vô.
Từ Sūnyā trong tiếng Ấn, nguồn gốc cho từ “zero,” đã bao trùm các khái niệm về không gian (space), sự trống rỗng (vacuousness), tính không đáng kể (insighificance) và các phi thực thể cũng như sự vô giá trị (worthlessness) và sự thiếu vắng (absence). Các truyền thống tôn giáo của Ấn Độ chấp nhận những khái niệm thần bí này hơn so với thế giới Phương Tây. Một người có thể đến từ hư vô và trở về với hư vô và trạng thái này cũng tương tự cho sự tồn tại. Robert Kaplan khẳng định: “Hư vô nằm ở trung tâm hệ tư tưởng của người Ấn và chúng ta tìm thấy sự suy đoán trong hầu hết các giai thoại vũ trụ về những gì đã tồn tại từ trước cả tạo hóa thế giới.” Do đó, việc một con số thể hiện rõ khái niệm Hư vô đến từ hệ thống toán học của người Ấn là hoàn toàn hợp lí.
Số Không du hành về Phương Tây
Hệ thống đếm của Ấn Độ có lẽ là phát kiến về mặt trí tuệ thành công nhất của con người. Phát minh này được chấp nhận trên toàn thế giới, là thứ gần nhất với ngôn ngữ quốc tế mà chúng ta có. Người Trung Quốc tiếp nhận hệ thống này của người Ấn vào khoảng thế kỉ 8 trước công nguyên và kế thừa số không dạng hình tròn cũng như cách ký hiệu số theo vị trí3 (place-value notation) với chín chữ số. Học giả người Do Thái Ben Ezra (1092 – 1167) đã mang con số không theo ông trong cuộc hành trình qua Châu Á và Phương Đông. Ông đổi tên con số không thành galgal hay “bánh xe” (wheel) bởi vì hình dạng tròn của nó.
Con số không của Ấn Độ đến với Châu Âu qua Tây Ban Nha theo những nhà buôn gia vị Ả Rập. Người Ả Rập giao thương mật thiết với Ấn Độ, và họ đánh giá cao tính hiệu quả của hệ thống đếm này, đến mức đưa nó vào sử dụng. Dần dần, con số không Ấn Độ được nhập vào hệ thống toán học và triết học phức tạp của người Ả Rập. Nhà toán học vĩ đại Al-Khwarizmi viết về kĩ thuật tính toán của người Ấn Độ như sau:
Sau khi trừ hết, họ điền một vòng tròn nhỏ, để vị trí đó không bị trống. Vòng tròn nhỏ phải chiếm vị trí đó, bởi vì nếu không thì sẽ còn ít chữ số hơn, và con số thứ hai có thể bị nhầm lẫn với con số thứ nhất.
Vào thế kỉ 11 và 12, nền văn minh Hồi giáo – Ả Rập có những khám phá khoa học sâu sắc và vươn tới những đỉnh cao của văn hóa. Đồng thời, Châu Âu đang tỉnh dậy giữa một cuộc tiểu phục hưng về văn hóa và khoa học của riêng nó. Vì dân số Châu Âu tăng vọt, các quân vương ra lệnh khai phá đất đai cho các thành thị lớn hơn, tầng lớp cai trị xây dựng những nhà thờ lộng lẫy và các tu viện to lớn. Song song với thời kì tiểu phục hưng này, giá cả hàng hóa tăng, số lượng tiền được đưa vào lưu thông cũng tăng và thương mại được phục hồi. Những thương gia Châu Âu cũng xuất ngoại thường xuyên hơn và tiếp xúc với khoa học Ấn Độ – Ả Rập, đáng chú ý hơn cả là hệ thống đếm khi trao đổi hàng hóa.
Thế giới Phương Tây lúc đó phần lớn bỏ qua khái niệm con số không, cho đến khi nhà toán học người Ý Fibonacci giới thiệu khái niệm ký hiệu 0 trong cuốn chuyên luận của ông vào năm 1202 Liber Abaci (The Book of Abacus, tạm dịch: Cuốn sách của Abacus) (Pogliani et al.). Fibonacci thời trẻ lớn lên tại bắc Phi, nơi cha ông quản lí một cơ quan hải quan và ông học được hệ đếm Ả Rập từ các gia sư người Hồi giáo. Từ khi còn trẻ, ông đã du ngoạn đến nhiều nơi ở vùng Địa Trung Hải, đến thăm những trung tâm về giáo dục và học thuật ở Ai Cập, Syria, Hy Lạp, Sicily và miền Nam nước Pháp. Do cha là một nhân viên hải quan, nên ông có nhiều cơ hội để quan sát nhiều hệ đếm khác nhau được sử dụng bởi các thương gia, mà đặc biệt là những nhà buôn Hồi giáo. Fibonacci nhanh chóng nhận ra lợi ích của hệ đếm Ả Rập – Ấn Độ và giới thiệu những con số mới bằng những dòng sau: “Chín chữ số Ấn Độ bao gồm 9, 8, 7, 6, 5, 4, 3, 2, 1. Với chín chữ số này và số không mà tiếng Ả Rập gọi là şifr thì bạn có thể viết bất cứ con số nào mà bạn muốn” (Joseph); và Fibonacci gọi số không là zephirum. Pogliani và các cộng sự đưa ra lập luận rằng chính Fibonacci đã giới thiệu hệ chữ số Ấn Độ – Ả Rập đến với toán học Châu Âu.
Gerbert d’Aurillac cũng có ảnh hưởng trong việc đưa số học Ấn Độ – Ả Rập đến những trung tâm học thuật ở Châu Âu. Sinh ra tại Aquitaine (miền Nam nước Pháp) vào khoảng năm 945, ông trở thành tu sĩ tại một tu viện ở Aurillac (Ifrah). Trong lúc ở Tây Ban Nha vào 967-970, ông làm quen với toán học, thiên văn học và hệ thống đếm của người Ả Rập. Tại Tu viện Santa Maria de Ripoll, ông bắt gặp việc ghép các nguyên tố Ả Rập vào một bài luận về Giáo hội Nguyên thủy4 (Primitive Church) được viết bởi Isidore5 tại Hội đồng Nicaea6. Ông vô cùng hứng thú với toán học Ấn Độ – Ả Rập và đi du hành khắp mọi nơi.
D’Aurillac giữ cương vị là hiệu trưởng trường giáo phận tại Reims và sau đó là cha trưởng tại Tu viện Bobbio ở Ý. Ông được bầu là Tổng giám mục của Reims và sau đó là Ravenna. Được bầu chọn là Đức giáo hoàng vào năm 999, Gerbert d’Aurillac lấy tên là Sylvester II (Sylvester Đệ Nhị). Ông sử dụng tầm ảnh hưởng của mình để chia sẻ những hiểu biết và niềm đam mê của mình đối với toán học Ấn Độ – Ả Rập. Ngày nay ông được biết đến như là học giả lớn đầu tiên truyền bá rộng rãi cách sử dụng các chữ số Ấn Độ – Ả Rập và máy đẳng cao7 (astrolabe) ở Châu Âu.
Số Không ngày nay
Các chính phủ châu Âu như Ý và Đức (trong một thời gian) vẫn giữ sự nghi ngờ đối với việc sử dụng con số không theo cách của Fibonacci, bởi vì quá dễ dàng để thay đổi một biểu tượng chữ số này sang biểu tượng chữ số khác. Các thương nhân đã sớm dựa vào con số không để cân bằng thu chi trong sổ sách kế toán, tuy nhiên, họ vẫn tiếp tục sử dụng số không trong những tin nhắn hay các dòng lệnh mã hóa. Đến đầu thế kỉ 16, thế giới Phương Tây đã đưa các chữ số Ấn Độ – Ả Rập vào sử dụng tiêu chuẩn trong số học. Kể từ đó, số học được giảng dạy ở các trường học ngày nay hầu như giống với những gì mà được dạy ở các trường học vào những năm 1500.
Tuy nhiên, con số không Ấn Độ – Ả Rập ảnh hưởng không chỉ đến số học; phát kiến số không và những ứng dụng của nó ảnh hưởng trực tiếp đến toán học và các ngành khoa học khác. Con số không là nền tảng để xây dựng nên hệ tọa độ Cartesian của Rene Descartes mà chúng ta sử dụng ngày nay. Isaac Newton và Gottfried Wilhelm von Liebniz dựa vào con số không để tạo nên phép tính tích phân, có lẽ là thành tựu cao quý nhất của toán học. Nếu không có nó thì chúng ta sẽ không có vật lý, kỹ thuật, khoa học máy tính và hầu hết các lý thuyết tài chính và kinh tế hiện đại.
Nếu không có nó thì chúng ta sẽ không có vật lý, kỹ thuật, khoa học máy tính và hầu hết các lý thuyết tài chính và kinh tế hiện đại.
Kết luận
Charles Seife lập luận rằng “bất cứ khi nào bạn có ký hiệu giữ chỗ, tức là bạn đang ám chỉ sự vắng mặt của một con số” (Matson). Con số không có lẽ được người Babylon, Maya và Ấn Độ tạo ra, một phương thức để đánh dấu những chỗ thiếu trong sổ cái. Tuy nhiên, trong khi các học giả Ấn Độ chật vật hòng tìm cách để thực sự định lượng và thể hiện số không, con số không vốn đã được định sẵn là sẽ trở thành bước ngoặt của sự phát triển, thiếu nó thì sự phát triển của khoa học hiện đại, công nghiệp hay thương mại khó trở thành sự thật (Dantzig).
Tầm ảnh hưởng của phát minh của số không không chỉ giới hạn trong phạm vi bộ môn số học. Phát kiến và quá trình phát triển của số không đã ảnh hưởng đến cách chúng ta hiểu về toán học và các ngành khoa học , từ sinh học cho đến thiên văn học. Trong lịch sử của các nền văn hóa, con số không sẽ được ghi nhận như là một trong những thành tựu trí tuệ vĩ đại nhất của loài người.
Nguồn tham khảo
Barrow, John D. 2000. The Book of Nothing: Vacuums, Voids, and the Latest Ideas about the Universe. New York, NY: Pantheon Books.
Boucenna, Ahmed. “Origin of the Numerals: Zero Concept.” Cornell University. July 24, 2007. Accessed November 22, 2013.
Dantzig, Tobias. 2005. Number: The Language of Science. New York, NY: PI Press.
Ifrah, Georges. 1985. From One to Zero: A Universal History of Numbers. New York, NY: Viking Penguin Inc.
Joseph, George Gheverghese. 2011. The Crest of the Peacock: Non-European Roots of Mathematics. Princeton, NJ: Princeton University Press.
Kaplan, Robert. “What Is the Origin of Zero? How Did We Indicate Nothingness before Zero?” Scientific American. January 16, 2007. Originally posted February 28, 2000. Accessed November 22, 2013.
Katz, Victor J. 1998. A History of Mathematics: An Introduction. 2nd Ed. Reading, MA: Addison Wesley Longman, Inc.
Matson, John. “The Origin of Zero.” Scientific American. August 21, 2009. Accessed November 22, 2013.
Pogliani, Lionello, Milan Randić, and Nenad Trinajstić. “Much Ado about Nothing?An Introductive Inquiry about Zero.” International Journal of Mathematical Education in Science and Technology. 1998. Vol. 29, No.5, pp. 729-744.
Rotman, Brian. 1987. Signifying Nothing: The Semiotics of Zero. New York, NY: St. Martin’s Press.
Đạo Jain, hay Jain Dharma, là một tôn giáo cổ thuộc dòng truyền thừa Śramaṇa ở Ấn Độ. Tư tưởng chính của tôn giáo này là không bạo lực và tôn trọng tất cả chúng sinh. ↩
Trong toán học, toán tử nói chung là một phép ánh xạ (một quy tắc tương ứng áp dụng lên hai tập hợp bất kỳ, mà trong đó mỗi phần tử của tập hợp này tương ứng với một và chỉ một phần tử thuộc tập hợp kia) hoạt động trên các phần tử của không gian để tạo ra các phần tử khác trong cùng không gian. Các toán tử phổ biến nhất là các bản đồ tuyến tính, tác động lên không gian véc tơ.↩
Ký hiệu số theo vị trí là một phương pháp để đại diện hoặc mã hoá số. Ký hiệu số theo vị trí được phân biệt với các ký hiệu khác (như các chữ số La Mã) để sử dụng cùng một biểu tượng cho các bậc độ lớn khác nhau. Điều này sẽ làm đơn giản hóa số học. ↩
Nhà thờ Cơ Đốc giáo thời kỳ đầu về bản chất và hình thức tổ chức trong ba thế kỷ đầu tiên sau công nguyên.↩
-
Thánh Isidore thành Hispalis (560 – 636) là một học giả và là Tổng giám mục thành Hispalis (Sevilla ngày nay) trong hơn ba thập kỷ. Ông thường được coi là một trong những Giáo phụ sau cùng, và được nhà sử học thế kỷ 19 Montalembert đánh giá là “học giả cuối cùng của thế giới cổ đại”.
Giữa thời kỳ suy thoái của văn hóa cổ điển, bạo lực giữa tầng lớp cai trị và nạn thất học, cùng với anh mình là Leander thành Hispalis, Isidore đã can dự đến sự cải đạo của người Visigoth theo phái Arius đang nắm quyền sang Công giáo. Ông cũng có ảnh hưởng trong triều đình Sisebut, vị vua người Visigoth của Hispania, đồng thời, có vai trò lớn trong Hội đồng Toledo và Sevilla.
Sau khi qua đời, danh tiếng của Isidore vẫn tiếp tục nhờ cuốn Etymologiae, một bách khoa toàn thư về nguồn gốc ngôn từ, chứa đựng các trích dẫn từ các sách kinh điển thời cổ đại.↩
Hội đồng Nicea (hay Hội đồng Nicea đầu tiên) là một hội đồng gồm những Giám mục cơ đốc giáo được triệu tập tại Nicea thuộc xứ Bithini (ngày nay là xứ Iznik của Thổ Nhĩ Kỳ) bởi Hoàng đế La Mã Constantine I vào năm 325 sau công nguyên. Hội đồng này có ý nghĩa lịch sử như là nỗ lực đầu tiên nhằm đạt đến sự thống nhất trong hội thánh Kitô giáo. Mục đích đầu tiên của việc triệu tập là nhằm tiêu diệt những người theo dị giáo Arian (nhấn mạnh thiên tính của Chúa Cha hơn Chúa Con), thống nhất thờ phượng ngày Lễ Phục Sinh và ban hành giáo luật↩
Máy đẳng cao là một thiết bị điều hướng thời cổ đại được sử dụng để xác định vị trí của Mặt trời và các ngôi sao vào một địa điểm cụ thể tại một thời điểm nhất định. ↩