Có phải tự nhiên vốn dĩ là ngẫu nhiên? Theo một số giải thích trong cơ học lượng tử, đúng là như vậy, và điều này lý giải vì sao chúng ta không thể tiên đoán chính xác chuyển động của các hạt đơn. Trong thí nghiệm hai khe hở nổi tiếng (theo như Richard Feynman tuyên bố, thí nghiệm này “là trái tim của ngành cơ học lượng tử”), chúng ta không thể dự đoán chính xác vị trí của một photon sau khi nó đi qua hai khe hở và rơi vào màn chắn phía sau. Nhưng ta có thể dự đoán cực kỳ chuẩn xác về sự phân bố của rất nhiều hạt, từ đó giả thuyết rằng, sau cùng, tự nhiên có lẽ đã được định sẵn. Quả thật, ta có thể dự đoán chính xác đến nhiều chữ số thập phân về sự phân phối của hàng tỷ photon khi bắn qua hai khe hở.

Sự đối lập giữa hành vi riêng lẻ không thể đoán trước và hành vi tổng thể chuẩn xác không còn lạ lẫm đối với ngành cơ học lượng tử. Vật lý lượng tử có nhiều khía cạnh kỳ lạ — chẳng hạn như lưỡng tính sóng-hạt, liên đới lượng tử (quantum entanglement) và nguyên lý bất định (uncertainty theory) — nhưng phương trình xác suất dự đoán chính xác hành vi tổng thể không phải một trong số đó. Chúng ta nhận thấy hiện tượng này ở bất cứ lĩnh vực nào có số lượng lớn các nhân tố tương tác lẫn nhau, chẳng hạn như trong nhiệt động lực học, ta có thể dự đoán chính xác những thông số vĩ mô như nhiệt độ và áp suất, trong khi hoàn toàn không hiểu về quá trình hoạt động của các phân tử đơn lẻ.

Trong câu đố tháng Tám, chúng ta đã tranh luận rằng quyết định luận1 hay sự ngẫu nhiên mới là quan trọng nhất trong cơ học lượng tử, cuộc tranh luận có thể được mô tả như là giữa nhóm B (Niels Bohr) và nhóm E (Albert Einstein). Nhóm B cho rằng sự không thể tiên đoán của hành vi hạt là chứng cứ cho thấy ở cấp độ sơ khai của vũ trụ, quyết định luận được thay thế bởi sự ngẫu nhiên mang tính khách quan và sẵn có. Nhóm E luận rằng sự ngẫu nhiên này chỉ là biểu hiện của sự thiếu hiểu biết của chúng ta về một cấp độ sâu sắc hơn trong quan hệ nhân quả.

Tháng này, chúng ta sẽ tìm hiểu hoạt động của một dụng cụ cơ học có thể minh họa sống động cách quy luật tất định tạo nên hành vi mang tính xác suất. Dụng cụ này được gọi là bảng Galton, hay máy phân loại đậu. Bước ảnh dưới phác họa một bảng Galton cổ điển, là một bảng thẳng đứng với các hàng chốt, tạo ra nhiều lối đi để viên bi rơi từ trên xuống dưới. Những viên bi được thả từ đỉnh và nảy sang trái hoặc sang phải khi chạm vào mỗi chốt. Ở phiên bản truyền thống của dụng cụ này, xác suất rơi sang trái hay sang phải là như nhau ở mọi chốt. Bi sẽ rơi xuống các thùng chứa từ 1 đến 8 được đặt dưới đáy.

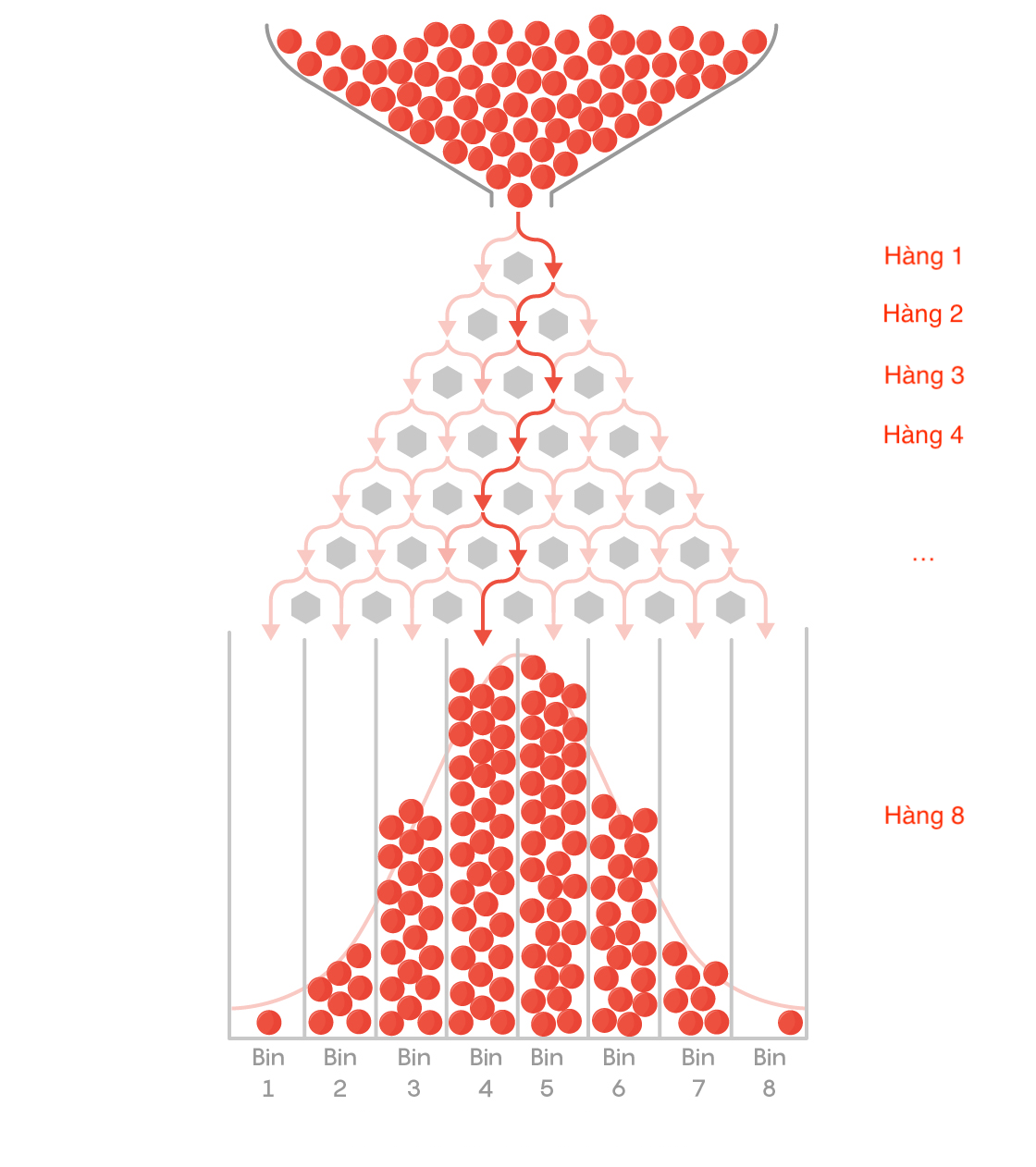
Số bi kỳ vọng thu được ở mỗi thùng từ trái qua phải sau khi đi qua tất cả đường đi có thể được tính bởi phân phối nhị thức. Để thực hiện một tập hợp đầy đủ những thử nghiệm với một bảng Galton và thùng chứa đặt ở hàng thứ n, ta cần tổng số bi là 2^(n-1). Nếu thùng đặt ở hàng đầu tiên (khi viên bi rơi thẳng vào thùng và không qua chốt nào), số bi là 2^(1-1) = 2^0 = 1, nếu đặt ở hàng 2, số bi là 2^1 = 2, nếu đặt ở hàng 3, số bi là 2^2 = 4, và cứ tiếp tục như vậy. Vì xác suất bi rơi sang trái hoặc phải là 50-50 ở mỗi chốt, số bi thu được ở mỗi thùng sẽ giống với sự phân phối khi tung đồng xu n-1 lần. Như vậy, một bảng Galton với thùng chứa đặt ở hàng thứ năm có thể được thực hiện bởi bốn lần tung xu, và cần 16 lần thử nghiệm bốn lần tung xu (tương ứng với 16 viên bi) để hoàn thành một tập hợp đầy đủ các thử nghiệm. Trong thùng, bạn sẽ thu được số bi tương ứng như sau: một trường hợp không có mặt ngửa nào (bốn mặt sấp), bốn trường hợp với một mặt ngửa, sáu trường hợp với hai mặt ngửa, bốn trường hợp với ba mặt ngửa, và một trường hợp với bốn mặt ngửa. (Chú ý rằng 16 là số thử tối thiểu để có được tỉ lệ trên. Trên thực tế, thực hiện càng nhiều thử nghiệm, kết quả càng gần đúng với tỉ lệ lý tưởng.)

Trong một bảng Galton với số hàng bất kì, số đường đi có thể của một viên bi tới thùng chứa ở một hàng cụ thể chính xác bằng các số tương ứng trong tam giác Pascal (như hình vẽ bên dưới). Khi số hàng chốt và số thùng tăng, sự phân phối của bi trong các thùng trông gần giống với đường cong chuông (bell curve). Do đó, những giả lập máy tính với bảng Galton quy mô lớn có thể minh họa trực quan về định lý giới hạn trung tâm (central limit theorem). Định lý này nói rằng khi số lượng thùng chứa tiến đến vô cùng, giới hạn về mặt lý thuyết của phân phối nhị thức là đường cong chuông (còn được gọi là phân phối Gauss).

Dĩ nhiên, không nhất thiết những viên bi phải rơi qua trái hoặc phải với xác suất bằng nhau. Ta có thể thiết kế các chốt sao cho xác suất này nằm trong khoảng từ 0 tới 1. Điều này cho phép bảng Galton có thể mô phỏng phân phối nhị thức hay nhiều dạng phân phối khác trong trường hợp phân phối bị lệch sang trái hoặc sang phải. Và điều đó đưa chúng ta đến với câu đố đầu tiên.

Câu đố 1: Những Chiếc Thùng Bình Đẳng

Hãy tưởng tượng bạn có một bảng Galton như hình vẽ trên. Bảng gồm thùng chứa đặt ở hàng thứ 8 và kiểu chốt truyền thống mà xác suất bi nảy sang hai bên là bằng nhau. Bạn muốn chỉnh sửa sao cho mỗi thùng đều thu được số bi bằng nhau. Bạn biết bạn phải thay thế một số chốt truyền thống bằng những chốt mới để hướng những viên bi sang trái hoặc phải với xác suất lệch nhau. Bạn có thể chọn loại chốt hướng tất cả bi sang trái, hướng tất cả sang phải, hoặc bất kì tỷ lệ nào ở giữa.

Số chốt nhỏ nhất mà bạn phải thay, và với tỉ lệ trái-phải là bao nhiêu, để số bi đựng trong mỗi thùng đều bằng nhau?

Đi cùng với đó là câu hỏi, bạn có thể tìm ra và chứng minh công thức tổng quát cho một bảng Galton với kích thước bất kì không? (Đối với bảng có số lẻ thùng chứa, hiệu số bi giữa hai thùng bất kì sau một thử nghiệm hoàn chỉnh nên là 1 hoặc 0. Theo như vậy, đối với một bảng Galton năm hàng và một bộ đủ 16 viên bi, số bi ở mỗi thùng phải là 3 hoặc 4.)

Ở bảng Galton truyền thống, phân phối bi ở mỗi hàng đạt đỉnh ở trung tâm và giảm dần về hai đầu. Ở câu đố tiếp theo, hãy thử xem chúng ta có thể tạo ra hai đỉnh không nhé.

Câu đố 2: Đỉnh núi đôi

Như ở Câu đố 1, bạn bắt đầu với bảng Galton truyền thống, nhưng lần này với chín thùng ở hàng cuối. Bạn phải chỉnh sửa nó bằng cách thay đổi số chốt tối thiểu sao cho bi được phân phối như sau: 0, x, 2x, x, 0, x, 2x, x, 0, với x là ⅛ tổng số bi.

Ở bảng Galton truyền thống, vị trí kết thúc một viên bi riêng lẻ khi di chuyển từ hàng giữa đến hàng cuối là không thể dự đoán — nó có thể kết thúc tại bất cứ thùng nào. Như bạn đã thấy, việc thực hiện chỉnh sửa trong hai câu đố trên khiến cho bảng Galton mang tính sắp đặt hơn so với trước đó. Giờ chúng ta có thể dự đoán đường đi của một viên bi độc lập chính xác hơn rất nhiều. Hãy thử định lượng khuynh hướng này nhé.

Câu đố 3: Dự đoán hành vi riêng lẻ

Ở bức ảnh trên, ta coi một viên bi có “hành trình” về 0 nếu nó ở một trong bốn vị trí ở hàng 4 và kết thúc tại vị trí tương ứng ở hàng 8, như chiều chỉ của mũi tên. Nếu viên bi kết thúc tại thùng chứa khác, giá trị của hành trình bằng bình phương khoảng cách từ thùng đó đến thùng chứa kỳ vọng. Theo như vậy, nếu một viên bi bắt đầu tại vị trí ngoài cùng bên trái ở hàng 4 và kết thúc tại thùng đánh số 7, khoảng cách đến thùng chứa kỳ vọng là một, hành trình của nó là 1^2 = 1. Nếu viên bi kết thúc tại thùng ngoài cùng bên trái ở hàng cuối (thùng đánh số 1), khi đó hành trình của nó là 2^2 = 4. Hành trình trung bình của một bảng Galton cụ thể bằng trung bình cộng của hành trình của các viên bi khi chúng di chuyển từ hàng 4 đến hàng 8.

Hành trình trung bình là bao nhiêu ở những bảng sau:

1. Bảng Galton truyền thống.
2. Bảng Galton đã chỉnh sửa trong câu đố 1.
3. Bảng Galton đã chỉnh sửa trong câu đố 2.

Trong bảng Galton truyền thống, tính ngẫu nhiên ở mỗi chốt — khả năng rơi sang trái hay phải của viên bi — có thể được sắp đặt thông qua các cơ chế thay đổi ngẫu nhiên theo thời gian ở từng chốt, hoặc qua những nhân tố tinh vi như vị trí ban đầu của bi, góc chuyển động, hoặc cách viên bi nảy khỏi bề mặt không hoàn hảo (imperfect surface) của chốt. Những nhân tố tiền định với một chuỗi sự kiện đầy tính nhân quả này sẽ ấn định đường đi của viên bi. Lối đi được chọn có vẻ ngẫu nhiên đối với chúng ta bởi lẽ chúng ta chẳng biết gì về những chi tiết này. (Một vài bảng Galton loại bỏ hoàn toàn tính bất tiền định và sắp đặt các cổng để thay đổi trạng thái của những viên bi sau mỗi lần chạm, từ đó họ có thể khiến viên bi đi theo một lối khác.)

Hãy áp dụng điều này cho câu hỏi triết học liên quan tới sự ngẫu nhiên và quyết định luận, theo như nhóm E lý giải. Đối với bảng Galton, chắc chắn tồn tại những quá trình nhân quả giống nhau quyết định xem một photon cụ thể sẽ kết thúc ở đâu trên màn chắn trong thí nghiệm hai khe hở. Chúng ta có thể không bao giờ hiểu được những quá trình này ra sao, nhưng chúng chắc chắn có tồn tại. Có lẽ điều này chẳng có ý nghĩa thực tế nào, nhưng nó chỉ ra rằng phương trình xác suất Schrödinger chỉ là một phương trình tổng quát giống như phương trình nhị thức mô tả một bảng Galton truyền thống. Nếu như vậy, phương trình này không có kết quả dự đoán nào cho một hạt đơn. Điều này làm suy yếu nền tảng của thuyết đa vũ trụ, thuyết này giả định rằng cả vũ trụ đang được nhân bản vô số lần mỗi khi một hạt nhỏ bé đưa ra một quyết định khác. Nếu phương trình này chỉ miêu tả hành vi tổng thể, viễn cảnh trên có vẻ không cần thiết. Như thể vũ trụ chia tách mỗi khi một viên bi nảy sang trái hoặc sang phải trong bảng Galton, chỉ vì chúng ta không hiểu được những chi tiết cụ thể về sự tương tác bi-chốt. Hỡi nhóm B, quan điểm của bạn đối với lời giải thích đơn giản này là gì?

Chúc bạn giải đố và tranh luận vui vẻ.

******

Lời của ban biên tập: Hãy để lại lời giải của bạn tại phần comment trong post Facebook này của zeal nhé. Câu trả lời sáng tạo hoặc hợp lý nhất (theo đánh giá của ban biên tập) đến hết Thứ 6, 27/03/2020 sẽ có cơ hội nhận được một phần quà nhỏ từ chúng mình.