Từ giấy bìa cứng và băng dính trong, Craig Kaplan gấp nên một khối hình dạng cầu tuyệt đẹp, tựa công trình của kiến trúc sư Buckminster Fuller, hay một dạng bóng đá mới lạ. Khối hình gồm 4 mặt thập nhị giác đều (đa giác với 12 cạnh và 12 góc bằng nhau), 12 hình thập giác đều (đa giác 10 cạnh bằng nhau), và 28 khoảng trống nhỏ có hình tam giác đều. Vấn đề là khối hình này, về lý thuyết, không tồn tại. Tổng thể những đa giác trên không thể giao nhau ở các đỉnh khối, và khối hình này sẽ không khép kín được.

Mô hình của Kaplan chỉ khả thi nhờ vào khả năng xê dịch có được khi ghép các hình bằng chất liệu giấy. Các mặt khối có thể hơi phồng một chút, và mắt thường gần như không nhận ra được. “Hệ số sai sót từ việc dùng chất liệu giấy ngoài đời thực biến những điều bất khả thi về mặt lý thuyết trở nên khả thi,” Kaplan, nhà khoa học máy tính tại Đại học Waterloo ở Canada, cho hay.

Đây là một ví dụ mới mẻ về lớp các vật thể toán học không ai ngờ tới do nhà toán học người Mỹ Norman Johnson tình cờ khám phá ra vào thập niên 60. Lúc đó, Johnson đang hoàn thiện công trình thu thập những khối đa diện chuẩn do triết gia Platon khởi xướng1 từ hơn 2.000 năm trước. Giữa hằng hà sa số những hình khối ba chiều, chỉ có 5 khối hình có thể được dựng nên từ các đa giác đều tương đẳng, gồm: tứ diện, lập phương, bát diện, thập nhị diện và nhị thập diện. Nếu các mặt của đa diện không nhất thiết cùng một loại đa giác, ta có thể tạo được thêm 13 khối đa diện bán đều Ác-si-mét từ các đa giác đều với điều kiện là chúng giao nhau theo cùng cách tại các đỉnh, cũng như tạo thêm được các lăng trụ (mặt đáy là hai đa giác tương đẳng, mặt bên là các hình vuông) và các “phản lăng trụ” (anti-prisms, mặt đáy là hai đa giác tương đẳng, mặt bên là các tam giác đều).

Vào năm 1966, khi còn ở Đại học Bang Michigan, Johnson đã tìm ra 92 khối khác được tạo nên chỉ từ các đa giác đều, ngày nay được gọi là các khối Johnson. Và theo chứng minh sau đó vài năm của nhà toán học người Nga Viktor Zalgaller, khi đó đang làm việc tại Đại học Tổng hợp Leningrad2, Johnson đã tìm ra hết tất cả các khối hình khả thi. Không thể tạo nên bất cứ khối hình kín nào từ các đa giác đều nữa.

Tuy nhiên, trong khi hoàn thiện danh sách các khối đa diện, Johnson nhận thấy có điều kỳ lạ. Ông đã tìm ra các khối đa diện từ việc ráp mô hình bằng giấy bìa các tông và dây chun. Do số lượng khối đa diện khả thi tương đối hạn chế, ông đã dự đoán sẽ nhanh tìm ra các khối còn sót lại. Một khi ông bắt đầu đặt các mặt khối đa diện vào đúng vị trí, theo lý thuyết, các mặt này sẽ khớp với nhau. Nhưng thực tế không phải như vậy. “Khi ghép một số lượng lớn các đa giác với nhau, không phải lúc nào ta cũng nhìn ra là khối mình ráp nên có chuẩn xác không,” Johnson nhớ lại.

Theo lời ông, hình mẫu có vẻ khớp, nhưng “tính toán lại thì ta có thể thấy rằng có gì đó không đúng.” Khi xem xét kỹ hơn, mặt hình vuông thì không thực sự vuông, hay một trong các mặt khối không được phẳng. Nếu gọt bớt các mặt thì chúng sẽ hoàn toàn khớp nhau, nhưng khi đó các mặt này lại không còn là đa giác đều nữa.

Nhưng lúc đó Johnson chỉ tập trung vào việc liệt kê các khối đa diện chuẩn, nên không để ý lắm những sai số nhỏ nhặt này. “Tôi tạm gác chúng sang một bên và tập trung vào những khối hình hợp lệ,” ông nói. Tuy nhiên, các khối hình gần-chuẩn vụn vặt này không chỉ thu hút hứng thú từ Kaplan và những người yêu toán học ngày nay, mà còn là một phần của lớp rộng lớn những trường hợp toán học sai lệch nhỏ.

Không có, và không thể có định nghĩa chính xác cho khái niệm “sai lệch nhỏ.” Một quy luật cứng nhắc và cố hữu sẽ không hợp lý trong đời thật chông chênh. Còn ở hiện tại, Kaplan dựa trên quy tắc nôm na sau để xác định các khối đa diện Johnson sai lệch nhỏ: “[Là] lỗi sai toán học thực tế vốn có trong khối hình, tương tự với sai số trong thực nghiệm, đến từ việc thực hành với các vật liệu trong thế giới thực và đôi bàn tay thiếu hoàn hảo của con người.” Hay nói cách khác, nếu ta ráp được một khối đa diện bất khả thi — nhưng gần khả thi đến mức ta có thể lách luật để tạo ra nó — thì khối đa diện này là một trường hợp sai lệch nhỏ. Ở các mảng khác của toán học, sai lệch nhỏ nghĩa là một trường hợp gần chút nữa là xảy ra, khiến ta ngạc nhiên hoặc lừa phỉnh ta, tựa như một trò đùa hay chơi khăm vậy.

Một số trường hợp sai lệch nhỏ trong toán học, tương tự các khối Johnson sai lệch nhỏ, đơn thuần là những sự thật thú vị vặt vãnh, còn một số khác lại có ý nghĩa sâu sắc hơn trong toán học và vật lý.

Những bài toán cổ3như cầu phương hình tròn hay nhân đôi khối lập phương đều thuộc chùm các trường hợp sai lệch nhỏ như vậy. Các bài toán trên đều có vẻ mời mọc trêu ngươi như thể có lời giải, nhưng cuối cùng đều được chứng minh là không thể giải được, giống như một khối hình tưởng như sẽ khép kín nhưng thực tế là không. Một số phép dựng hình bằng thước kẻ và compa4 của Leonardo da Vinci và Albrecht Dürer đã làm sai lệch một số góc, tạo nên các đa giác gần đều thay vì hoàn toàn đều.

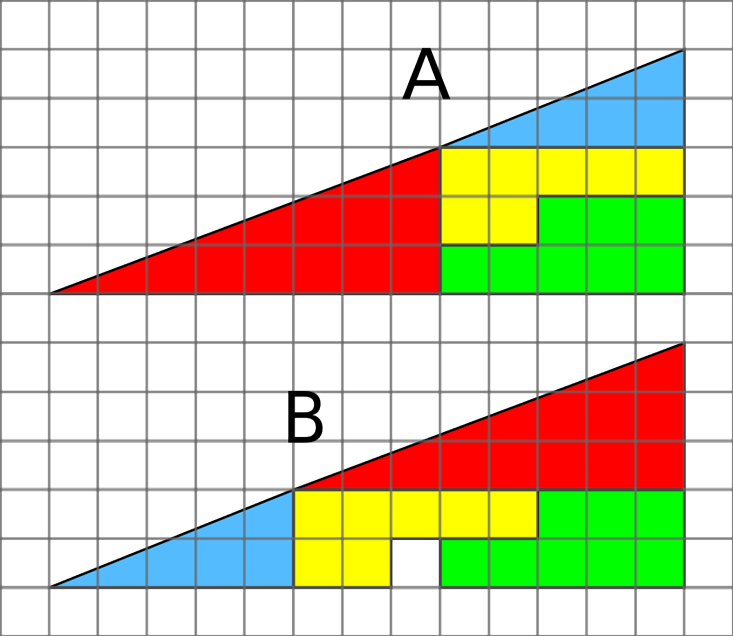
Và rồi đến bài toán ô vuông biến mất. Trong bài toán này (như trên hình), một tam giác vuông được cắt thành 4 phần. Khi các phần được sắp xếp lại, một khoảng trống xuất hiện. Khoảng trống này từ đâu ra vậy? Lại là một trường hợp sai lệch nhỏ. Không có hình “tam giác” nào ở đây cả. Phần cạnh huyền không thẳng mà hơi gấp khúc, hệ số góc là 0,4 ở tam giác màu xanh và đổi sang 0,375 ở tam giác màu đỏ. Vì biến đổi này gần như không thể phát hiện ra bằng mắt thường, nên ảo giác này gây ấn tượng mạnh.

Một trường hợp sai lệch nhỏ có lẽ là hữu ích nhất trong đời sống thường ngày là sự trùng hợp số học giữa 2^7/12 và 3/2. Hệ quả của sai lệch nhỏ này là mỗi quãng tám5 tương ứng với 12 phím đàn piano, và cũng là nền tảng cho bình quân luật trong âm nhạc phương Tây. Đây là sự thoả hiệp giữa hai quãng âm quan trọng nhất trong âm nhạc: quãng tám (tỉ lệ tần số là 2:1) và quãng năm (tỉ lệ tần số là 3:2). Về mặt số học, không thể chia quãng tám thành các quãng năm chuẩn được. Nhưng ta có thể đạt được kết quả gần chính xác bằng cách chia đều quãng tám thành 12 nửa cung, bảy nửa cung có tỉ lệ tần số là 1,498. Đối với hầu hết mọi người thì như vậy đã đủ tốt rồi.

Đôi khi các trường hợp sai lệch nhỏ phát sinh trong nội tại toán học, như thể toán học đang tự chơi khăm chính mình vậy. Trong tập “Treehouse of Horror VI” (tạm dịch: Căn nhà cây rùng rợn phần 6) trong chương trình Gia đình Simpsons, một số khán giả yêu thích toán có thể đã để ý thấy phương trình kỳ lạ 1782¹² + 1841¹² = 1922¹². Trong một khắc, dường như các nhà biên kịch đã phủ định Định lý lớn Fermat6, rằng phương trình có dạng xⁿ + yⁿ = zⁿ không tồn tại nghiệm nguyên khi n lớn hơn 2. Nếu bấm các con số ở trên vào máy tính cầm tay thì phương trình này có vẻ chính xác. Nhưng nếu tính toán chi li hơn cả hầu hết các máy tính cầm tay, ta sẽ ra được căn bậc mười hai của vế bên trái phương trình là 1921,999999955867… chứ không phải 1922, và Fermat có thể yên nghỉ rồi. Trường hợp sai lệch nhỏ này thật đáng kinh ngạc — sai số chỉ chưa đến 1 trên 10 triệu.

Nhưng các trường hợp sai lệch nhỏ không chỉ là trò đùa vui. Theo nhà toán học John Baez từ Đại học California-Riverside, “những trường hợp khiến tôi hứng thú nhất có thể là manh mối trong một bức tranh lớn hơn.” Ví dụ như trường hợp một con số đôi khi được gọi là hằng số Ramanujan. Đó là số e^π√163, xấp xỉ bằng 262.537.412.640.768.743,99999999999925 — tiệm cận giá trị số nguyên một cách đáng kinh ngạc. Theo tiên nghiệm, chả có lý do gì để dự đoán rằng những số vô tỉ này — e, π, và √163 — có thể được kết hợp để tạo ra một số hữu tỉ chứ nói gì đến số nguyên. Có một lý do khiến sai lệch nhỏ đến như vậy. “Đây không phải là sự trùng hợp không thể lý giải, mà là manh mối dẫn tới một phần sâu hơn của toán học,” Baez nói. Phần lý giải chính xác hết sức phức tạp, nhưng phụ thuộc vào việc con số 163 ở trên thuộc nhóm số Heegner. Các hàm số mũ liên quan tới nhóm các số này đều có giá trị gần nguyên.

Hay thử xem xét mối quan hệ toán học được biết đến với cái tên sang chảnh “Monstrous Moonshine” (tạm dịch: Mặt trăng Quỷ quái). Chuyện là năm 1978, nhà toán học John McKay quan sát được một hiện tượng vừa vụn vặt tầm thường lại cụ thể một cách kỳ lạ: 196.884 = 196.883 + 1. Con số đầu tiên, 196.884 là một hệ số trong một đa thức quan trọng có tên j-invariant (tạm dịch: hàm j bất biến), còn số 196.883 có liên quan với một vật thể toán học khổng lồ có tên Monster group (Nhóm Quỷ). Nhiều người chắc sẽ nhún vai bỏ qua, nhưng những quan sát này đã khiến một số nhà toán học hứng thú và quyết định xem xét kỹ hơn. Họ khám phá ra các mối liên hệ giữa hai chủ đề tưởng chừng như chả liên quan này: lý thuyết số và tính cân đối của Nhóm Quỷ. Những mối liên kết này có thể còn có ý nghĩa thậm chí rộng lớn hơn nhưng chưa được khám phá với những chủ đề khác. Nhà vật lý Edward Witten cho rằng Nhóm Quỷ có thể liên quan tới hấp dẫn lượng tử và cấu trúc sâu của không-thời gian.

Những trường hợp sai lệch nhỏ trong toán học cho thấy sức mạnh và tính khôi hài của yếu tố con người trong toán học. Johnson, Kaplan, và nhiều người khác đã tìm ra chúng thông qua phép thử và sai – từ việc khám phá, như những nhà sinh vật học mò mẫm tìm các giống loài mới nơi khu rừng nhiệt đới. Nhưng với toán học, việc tìm kiếm có hệ thống có thể sẽ dễ dàng hơn. Chẳng hạn như trường hợp Jim McNeill, một người yêu thích toán học chuyên thu thập các trường hợp sai lệch nhỏ trên trang mạng của mình, và Robert Webb, một lập trình viên máy tính, đã phát triển phần mềm tạo lập và nghiên cứu các đa diện.

Các tình huống sai lệch nhỏ sống trong ranh giới âm u giữa toán học lý tưởng, không nhượng bộ với các giác quan nuông chiều và thực dụng của ta. Các tình huống này đảo nghịch lô-gích của sự xấp xỉ. Thế giới thực cơ bản là cái bóng không hoàn hảo của thế giới lý tưởng của Platon7. Tính chuẩn xác của toán học cơ bản bị mất đi trong điều kiện thực tế. Nhưng với những trường hợp sai lệch nhỏ, thế giới thực trở thành cái bóng hoàn hảo của thế giới không lý tưởng ở trên. Sự xấp xỉ là “phiên bản ước tính không-chính-xác của câu trả lời đúng,” trong khi “sai lệch nhỏ là đại diện chính xác của câu trả lời gần-đúng,” Kaplan cho hay.

Theo cách này, các trường hợp sai lệch nhỏ biến đổi mối quan hệ giữa nhà toán học và nhà vật lý toán học với thế giới tự nhiên. “Tôi biết ơn những khiếm khuyết của thế giới thực đã cho phép tôi đạt được trạng thái gần-hoàn-hảo với các đối tượng mà tôi biết rằng nội tại không hoàn hảo,” Kaplan nói. “Các khiếm khuyết cho phép tôi vượt qua những giới hạn của toán học nhờ sự vụn vỡ đẹp đẽ của hiện thực.”